
A Walk-through arrow maze is traversed by moving from intersection to intersection until the goal intersection is reached. As each intersection is approached from a given direction, a sign near the entry to the intersection indicates in which directions the intersection can be exited. These directions are always left, forward or right, or any combination of these.
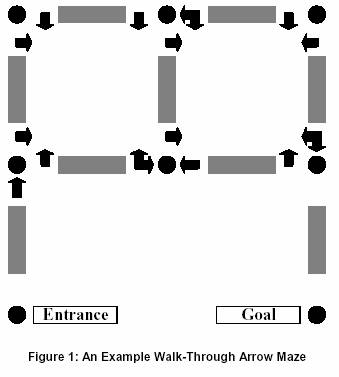
Figure 1 illustrates a walk-through arrow maze. The intersections are identified as (row, column) pairs, with the upper left being (1,1). The Entrance intersection for Figure 1 is (3,1), and the Goal intersection is (3,3). You begin the maze by moving north from (3,1). As you walk from (3,1) to (2,1), the sign at (2,1) indicates that as you approach (2,1) from the south (traveling north) you may continue to go only forward. Continuing forward takes you toward (1,1). The sign at (1,1) as you approach from the south indicates that you may exit (1,1) only by making a right. This turns you to the east now walking from (1,1) toward (1,2). So far there have been no choices to be made. This is also the case as you continue to move from (1,2) to (2,2) to (2,3) to (1,3). Now, however, as you move west from (1,3) toward (1,2), you have the option of continuing straight or turning left. Continuing straight would take you on toward (1,1), while turning left would take you south to (2,2). The actual (unique) solution to this maze is the following sequence of intersections: (3,1) (2,1) (1,1) (1,2) (2,2) (2,3) (1,3) (1,2) (1,1) (2,1) (2,2) (1,2) (1,3) (2,3) (3,3).
You must write a program to solve valid walk-through arrow mazes. Solving a maze means (if possible) finding a route through the maze that leaves the Entrance in the prescribed direction, and ends in the Goal. This route should not be longer than necessary, of course.
The input file will consist of one or more arrow mazes. The first line of each maze description contains the name of the maze, which is an alphanumeric string of no more than 20 characters. The next line contains, in the following order, the starting row, the starting column, the starting direction, the goal row, and finally the goal column. All are delimited by a single space. The maximum dimensions of a maze for this problem are 9 by 9, so all row and column numbers are single digits from 1 to 9. The starting direction is one of the characters N, S, E or W, indicating north, south, east and west, respectively. All remaining input lines for a maze have this format: two integers, one or more groups of characters, and a sentinel asterisk, again all delimited by a single space. The integers represent the row and column, respectively, of a maze intersection. Each character group represents a sign at that intersection. The first character in the group is N, S, E or W to indicate in what direction of travel the sign would be seen. For example, S indicates that this is the sign that is seen when travelling south. (This is the sign posted at the north entrance to the intersection.) Following this first direction character are one to three arrow characters. These can be L, F or R indicating left, forward, and right, respectively.
The list of intersections is concluded by a line containing a single zero in the first column. The next line of the input starts the next maze, and so on. The end of input is the word END on a single line by itself.
For each maze, the output file should contain a line with the name of the maze, followed by one or more lines with either a solution to the maze or the phrase .No Solution Possible.. Maze names should start in column 1, and all other lines should start in column 3, i.e., indented two spaces. Solutions should be output as a list of intersections in the format .(R,C). in the order they are visited from the start to the goal, should be delimited by a single space, and all but the last line of the solution should contain exactly 10 intersections.
The first maze in the following sample input is the maze in Figure 1.

2) Help the child out!
There is a cube, such that it’s each face has a different colour.The cube is further divided into 3 layers in all the 3 directions(i.e x,y,z axis)
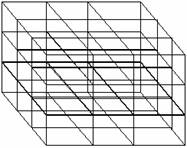
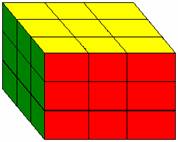
Cross Section of the cube Initial view of the cube(fig 1)
Also each layer can be rotated clockwise or anticlockwise.
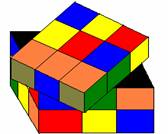
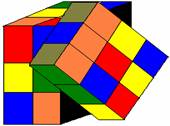
Initially, the cube is such that each face has it’s respective colour(Fig1).
A child playing with the cube, destructs its symmetry.The problem is to restore the cube to its original status.
Rules :
1) All layers must be able to move clockwise or anticlockwise controlled either by mouse or keyboard.
2) The unsymmetric state of the cube could either be generated by the computer or can be taken as a input from the user, provided it’s a valid state from which the original state of the cube can be restored.
3) Choice of the colours is up to the programmer.
4) A step by step solution for the problem ,if provided, will fetch extra points.
Rules and Regulations:
1.
All entries should be mailed to the E-mail Ids mentioned below latest
by
not be accepted.
2. The maximum number of students per team is three.
3. The students are free to attempt either one or both the problems listed
above, an on any platform (Windows, Linux) and in any language of their
choice (C, C++, VB, VC, Java).
Note: No. of problems attempted will count in the final judgment.
4. All participants
must reach the venue on
register their teams at the registration desk.
5. The teams should bring their source codes & executable files along with the
documentation and a brief presentation of their solutions.
6. For Open Software, in which the teams may demonstrate any software developed by
them, the teams have to register separately latest by the date & time specified above
by sending an E-mail to the ID given below or contacting the persons concerned.
E-mail id:
For Pre Defined
Software (
For Open Software : opensoftware_amitech03@yahoo.co.in
Contact persons: Mayank Sharma Varun Gupta
mayanksharma@hotpop.com varungupta12@hotmail.com
Tel: 26135435 Tel:26173602
www.amity.edu/amitech